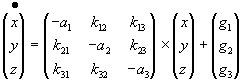
3. Lineare Erweiterungen des Richardson-Modells

3.1 Modelle dreier Staaten

Die Dimension des klassischen Modells von Richardson ist zwei; sie läßt sich aber beliebig vergrößern Der Fall von drei Staaten, oder drei Gruppen von Staaten, ist in der Wirklichkeit ebenso vorhanden wie der Fall zweier verfeindeter Staaten oder Staatengruppen. In der Praxis sind es oft zwei Machtblöcke, die besonders verfeindet sind, während eine Gruppe von mehr oder weniger neutralen Beobachtern sich mäßig rüstet und bereit hält, wie es zum Beispiel die Rolle der USA im Jahr 1938 war.

Die Literatur, auf die ich mich beziehe, ist einerseits Richardsons "Arms and Insecurity", andererseits ein Artikel von John E. Hunter: "Mathematical Models of a Three-Nation Arms Race"⁷. Dieser Artikel behandelt zwar keine Differentialgleichungen, aber seine Idee läßt sich direkt übertragen.

3.1.1 Modell dreier verfeindeter Staaten

3.1.1.1 Die Modellgleichungen

Das Modell ist die direkte Übertragung des zweidimensionalen Richardsonmodells auf den dreidimensionalen Fall. Jeder Staat (oder jede Staatengruppe) ist mit jedem anderen Staat (oder jeder anderen Staatengruppe) verfeindet und rüstet deshalb auf. Die Rüstungsausgaben der drei Staaten sind x, y und z. Die Bedrohungsparameter heißen k_ij, i,j =1, 2, 3, die Sättigungsparameter a_i und die Feindseligkeitsparameter g_i, i = 1, 2, 3. Damit erhält das Differentialgleichungssystem seine Gestalt.

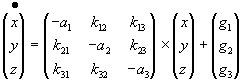(3.1)

Die Darstellung durch Kausalschleifen ist ebenfalls möglich.

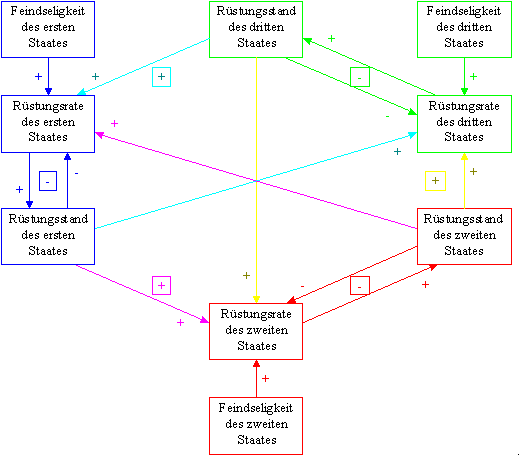
Abbildung 3.1 Modell dreier verfeindeter Staaten mit Kausalschleifen

Die Abbildung 3.1 weist einige Kausalschleifen auf. Diejenigen, die den Zusammenhang zwischen Rüstungsstand und Rüstungsrate eines Landes zeigen, sind negative Rückkoppelungen. Alle anderen Kreisläufe in diesem Modell weisen jedoch lauter "+" auf. Es kann zu negativen Rückkoppelungen, zu instabilem Verhalten kommen.

3.1.1.2 Gleichgewichtslagen und Stabilität

Beispiel

Wegen der größeren Dimension ist die Berechnung der Gleichgewichtslage und ihrer Stabilität nicht mehr so einfach. Gesetzt den Fall, daß sowohl die Bedrohungsparameter, die Sättigungsparameter und die Feindseligkeitsparameter der drei Staaten gleich sind, läßt sich jedoch ein Ergebnis leicht berechnen.

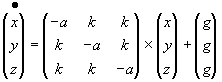(3.2)

Dieses einfache System läßt sich leicht untersuchen. Wir interessieren uns vor allem für die Gleichgewichtslage und deren Stabilität sowie für mögliche Lösungen der Differentialgleichungen.

Die Koordinaten der Gleichgewichtslage berechnen wir durch die Gleichsetzung der linken Seite mit 0, denn wir suchen ja den Punkt im Raum, an dem sich nichts mehr verändert, an dem die erste Ableitung 0 ist. Die Lösung ist ein Vektor, dessen einzelne Koordinatenwerte gleich sind. Das war wegen der Symmetrie der Rüstungsausgaben zu erwarten.

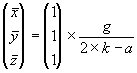(3.3)

Hier ist zu beachten, daß die Koordinatenwerte nur dann positiv sind, wenn 2×k - a > 0 ist, also wenn 2×k > a. Im gegenteiligen Fall ist das Ergebnis zwar mathematisch richtig, aber für die Praxis nicht interpretierbar und daher unwichtig.

Ist die berechnete Gleichgewichtslage stabil? Die Antwort liefert die nähere Betrachtung der Eigenwerte der Matrix.

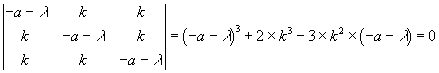(3.4)

Aus der Gleichung dritten Grades in (-a-l) können wir bequem l berechnen. Es ergibt sich:

(3.5)

(3.6)

Die Gleichgewichtslage ist assymptotisch stabil, wenn s₁ < 0 und s_2,3 < 0, was unter anderem bedeutet, daß 2×k < a sein soll. Das widerspricht aber der Bedingung für ihre praktische Existenz. Die real existiernde Gleichgewichtslage ist also nicht stabil.

Aus den Eigenwerten können wir auch die Lösung des vorliegenden Differentialgleichungssystems bestimmen. Zunächst setzen wir die unbestimmte Lösung an.

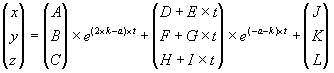(3.7)

Durch Einsetzen in das Differentialgleichungssystem erhalten wir Bedingungen, wie die unbestimmten Parameter A bis I voneinander abhängen.

(3.8)

(3.9)

(3.10)

(3.11)

In weiterer Folge setzen wir t₀ = 0 in die Lösung ein und bestimmen auf diese Weise mit Hilfe der Anfangswerte x₀, y₀ und z₀ jene Lösung, die durch diesen Anfangspunkt verläuft. So erhalten wir für die Parameter A bis I Werte, die von x₀, y₀ und z₀ abhängen und die Lösung eindeutig festlegen. Schließlich ergibt sich:

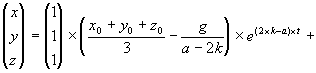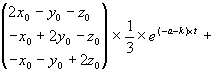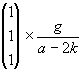(3.12)

Das war also der einfachste Fall, daß die entsprechenden Parameter der verschiedenen Staaten gleich groß sind. Er ist sicher nicht sehr wirklichkeitsnah, zeigt aber die prinzipiellen Möglichkeiten der theoretischen Untersuchung auf übersichtliche Weise. Die Vorgangsweise bleibt in jedem Fall die gleiche, auch wenn der Rechengang wesentlich komplizierter wird. Wenn allerdings die Parameter der Differentialgleichung bekannt sind, so ist die numerische Berechnung besonders einfach.

3.1.1.3 Implementation und Ergebnisse

Daß es in diesem Modell sowohl stabile als auch instabile Gleichgewichtslagen gibt, läßt sich ohne explizite Rechnung auch durch Simulation in HYBSYS zeigen. Wenn die Sättigungsparameter nur entsprechend groß gegenüber den Bedrohungsparamtern sind, so streben die Rüstungsausgaben einem endgültigen Wert zu, andernfalls wachsen sie exponentiell an.

Die Abbildung 3.2 zeigt den Verlauf der Rüstung, wenn eine stabile Gleichgewichtslage existiert. Nach einer relativ kurzen Zeit erreichen x, y und z die Werte von , und und bleiben auf diesem Stand. Ein Phasenbild kann in der zweidimensionalen Darstellung nur unvollständig sein; aber die Art, wie die Trajektorien der Gleichgewichtslage zustreben, ist eindeutig, wie wir in Abbildung 3.3 und Abbildung 3.4 sehen können, die einmal die Lage in der (x, z)-Ebene zeigen, einmal in der (y, z)-Ebene. Die Art, wie die Trajektorien ziemlich direkt der Gleichgewichtslage zustreben, ist beeindruckend.

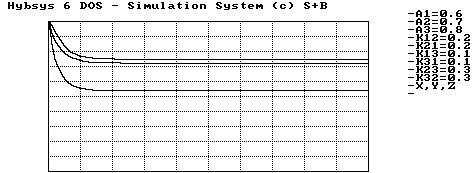
Abbildung 3.2 Stabile Gleichgewichtslage des Rüstens, Abrüstung

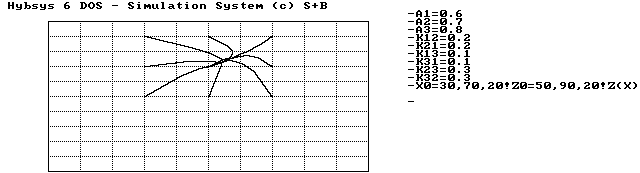
Abbildung 3.3 Phasenbild eines stabilen Gleichgewichtspunktes

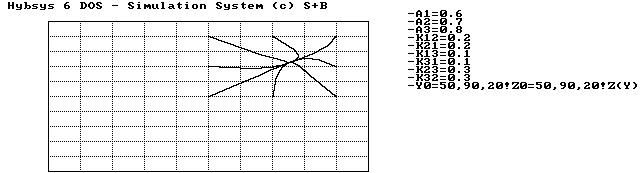
Abbildung 3.4 Phasenbild eines stabilen Gleichgewichtspunktes

Es gibt auch den Fall der Instabilität in diesem Modell. Wenn die Bedrohungsparameter groß genug gegenüber den Sättigungsparametern sind, dann rüsten alle drei Staaten exponentiell auf. Die Furcht vor den Gegnern vergrößert die Anstrengungen des Aufrüstens. Wegen des gegenseitigen Mißtrauens werden die militärischen Aktivitäten des Feindes genau beobachtet und die Konsequenzen der eigenen Aktivität gezogen. So schaukeln sich die Rüstungsausgaben gegenseitig auf.

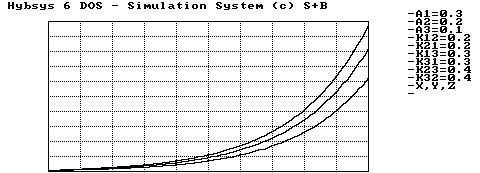
Abbildung 3.5 Instabiler Rüstungswettlauf, exponentielles Aufrüsten

3.1.2 Modell einer Allianz

3.1.2.1 Die Modellgleichungen

Wenn nun ein Staat mit einem anderen eine Allianz eingeht und sich mit ihm gegen den dritten verbündet, so hat das natürlich Auswirkungen auf das Modell. Die beiden befreundeten Staaten fürchten einander nicht mehr, ihre Aufrüstungsrate steigt nur mehr mit der Rüstung des dritten. Durch die Aufrüstung des Verbündeten fühlen sie sich nicht mehr bedroht, sondern geschützt. Die entsprechenden Bedrohungsparameter werden somit negativ und sind daher eigentlich Sättigungsparameter. Das drückt sich auch mit den veränderten Buchstaben a_ij und a_ji aus. Das Differentialgleichungssystem erhält folgende Gestalt:

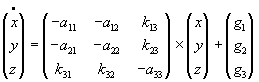(3.13)

Die Abbildung 3.6 zeigt die Darstellung des Modells mit Kausalschleifen. Obwohl in den Beziehungen der ersten beiden Staaten die entsprechenden Pfeile mit einem "-" gekennzeichnet sind, ist die entstehende Kausalschleife dennoch eine positiv rückgekoppelte, denn die Anzahl der "-" ist zwei, also gerade, und daher heben sie einander auf. Wieder müssen wir die Größe der Koeffizienten näher betrachten, um über die Stabilität der Gleichgewichtslage eine Aussage machen zu können.

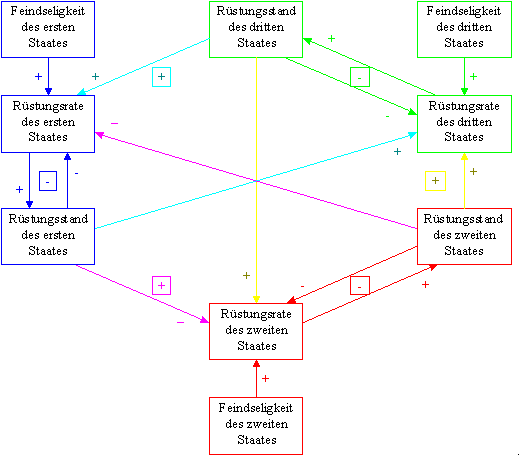
Abbildung 3.6 Modell einer Allianz durch Kausalschleifen dargestellt

Beispiel

Um die Rechnung einfach zu machen, nehme ich wieder einfache Parameterwerte an. So läßt sich auf unkomplizierte Weise ein Beispiel darstellen und seine Ergebnisse finden.

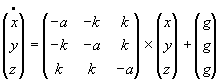(3.14)

Die Sättigungsparameter a₁₂ und a₂₁ habe ich mit Absicht nicht mit dem Wert a sondern mit k belegt, um die Zeilen der Matrix nicht linear abhängig zu machen. Dadurch kann ich in gewohnter Weise vorgehen und die Gleichgewichtslage, die Eigenwerte der Matrix und die Stabilitätsbedingungen ermitteln.

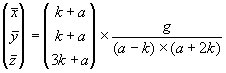(3.15)

(3.16)

(3.17)

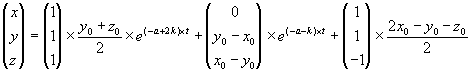(3.18)

Die Gleichgewichtslage existiert, wenn a > k ist. Die Stabilitätsbedingungen lauten:

und

(3.19)

Die zweite Ungleichung ist sicher erfüllt, denn wir setzen a und k als positiv voraus. Wenn a > 2k ist, ist auch a > k, und die Gleichgwichtslage existiert in dem für uns interessanten Bereich und ist überdies stabil.

3.1.2.2 Implementation und Ergebnisse

Abbildung 3.7 und Abbildung 3.8 zeigen die Ergebnisse der Simulation.

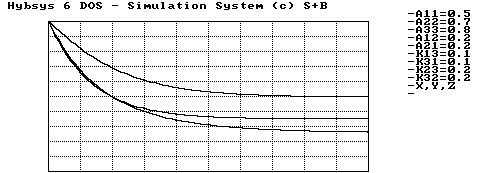
Abbildung 3.7 Stabile Gleichgewichtslage, Abrüstung

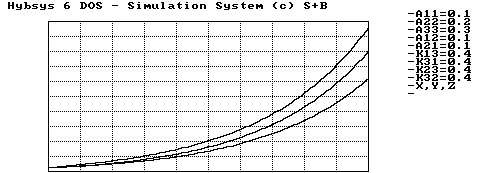
Abbildung 3.8 Instabiler Rüstungswettlauf

Das HYBSYS-Model unterscheidet sich von dem aus 3.1.1.3 nicht so stark, daß ich es hier anführen müßte. Die Bezeichnungen der Parameter und der Variablen sind gleichlautend mit denen der Modellgleichung (3.13).

3.1.3 Modell zweier Allianzen

3.1.3.1 Die Modellgleichungen

Um alle mathematischen Möglichkeiten auszuschöpfen, betrachten wir auch den Fall, daß es einem Staat gelingt, mit den beiden anderen Staaten eine heimliche Allianz zu schließen. Alle Koeffizienten in der Gleichung dieses Staates werden negativ, so wie auch die Koeffizienten in den anderen Gleichungen, die sich auf ihn beziehen.

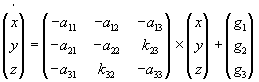(3.20)

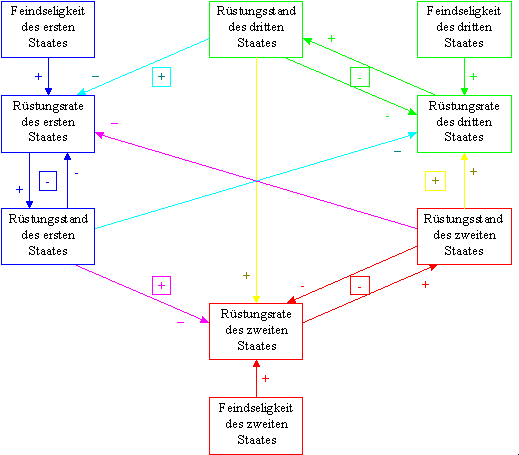
Abbildung 3.9 Modell zweier Allianzen mit Kausalschleifen

Es zeigt sich auch hier, daß wir nicht ohne weiteres auf das Vorhandensein einer stabilen Gleichgewichtslage schließen dürfen, ohne daß wir die Koeffizienten genauer betrachtet haben. Ihre Vorzeichen allein reichen nicht aus, weil die Veränderung von positivem zu negativem Vorzeichen wegen der Gegenseitigkeit von Allianzen immer paarweise auftritt.

Beispiel

Auch hier gibt es einen einfachsten Fall, der sich zur Veranschaulichung von theoretischen Betrachtungen eignet. Allerdings sollten die a_ij nicht nur untereinander gleich sein, sondern auch den selben Wert wie die k_lm haben, um die Berechnung der Eigenwerte wirklich zu vereinfachen. Zunächst einmal gibt es eine Gleichgewichtslage, weiters lassen sich Eigenwerte der einfachen Matrix berechnen.

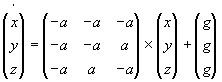(3.21)

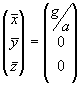(3.22)

(3.23)

(3.24)

Da l₁ = a per definitionem größer als 0 ist, ist die Gleichgewichtslage sicher nicht stabil. Mit einem unbestimmten Ansatz und Einsetzen eines Anfangswertes zum Zeitpunkt t₀ = 0 läßt sich eine explizite Lösung der Differentialgleichung finden.

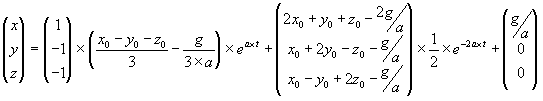(3.25)

3.1.3.2 Implementation und Ergebnisse

Wiederum unterscheidet sich das HYBSYS-Model nicht so stark von dem aus 3.1.1.3, bis auf die Bezeichungen und Vorzeichen einiger Koeffizienten.

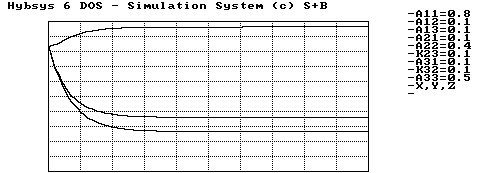
Abbildung 3.10 Stabiles Gleichgewicht

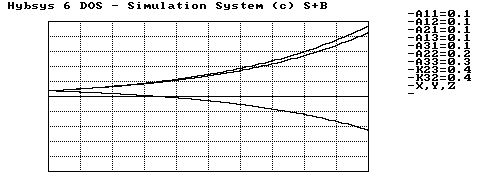
Abbildung 3.11 Instabiler Rüstungswettlauf

Die Abbildung 3.10 zeigt, daß es auch in diesem Modell den Fall gibt, daß die Rüstungsausgaben aller drei Staaten einen konstanten Wert erreichen. Die Kurve des ersten Staates, der mit beiden anderen verbündet ist, unterscheidet sich ein wenig von den anderen Kurven. Im Fall eines Wettrüstens gibt es ein noch viel seltsameres Resultat. Aus der Tatsache, daß alle Koeffizienten der Gleichung des ersten Staates negativ sind, ergibt sich der negative Verlauf der Kurve von x, wie wir in Abbildung 3.11 sehen können. Obwohl wir im Fall verfeindeter Staaten einen negativen Rüstungsstand nicht deuten könnten, läßt sich hier der negative Stand vielleicht als das Unterstützen beider befreundeter Staaten mit Waffen deuten. Wichtig ist vor allem, daß der Betrag von x nicht so groß ist wie der von y oder z.

3.2 Modell von n Staaten

So wie wir das erste Modell von Richardson auf drei Staaten ausgeweitet haben, können wir es auch auf beliebig viele tun. Der allgemeinste Ansatz ist n-dimensional. Die Staaten können in irgendeiner Weise verbündet sein und daher werden die entsprechenden Koeffizienten negativ. Sind aber alle Staaten verfeindet, so sind alle Elemente der Matrix der Differentialgleichung außerhalb der Diagonale positiv. Die Matrix will ich hier der Kürze wegen mit A bezeichnen.

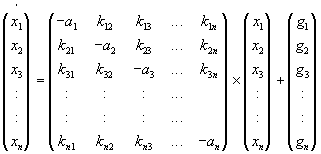(3.26)

(3.27)

Ob dieses System eine Gleichgewichtslage hat, hängt von der Determinante der Matrix A ab. Sie darf nämlich nicht 0 sein, die Zeilen oder Spalten der Matrix dürfen nicht linear abhängig sein. Die Gleichgewichtslage erhalten wir mit Hilfe der bekannten Regel von Cramer, die Werte der einzelnen Koordinaten lauten:

(3.28)

Ich möchte kurz ins Gedächtnis zurückrufen, was die Adjunkte⁸ eines Matrizenelementes a_ij eigentlich ist. Sie ist jene Unterdeterminante der Matrix, die durch Streichung der i-ten Zeile und der j-ten Spalte entsteht, multipliziert mit -1, wenn i + j eine ungerade Zahl ist.

(3.29)

Beispiel

Auch hier möchte ich ein spezielles Beispiel untersuchen. Angenommen, die entsprechenden Parameter der verschiedenen Staaten sind gleich groß, so hat die Gleichung eine besonders einfache Gestalt. Die Koordinaten des Gleichgewichtspunktes sind natürlich alle gleich groß.

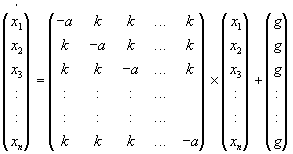(3.30)

(3.31)

Es bleiben noch die Eigenwerte der Matrix zu berechnen, um die Stabilitätsbedingungen zu ermitteln.

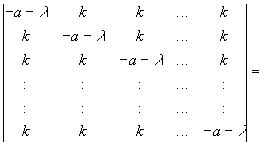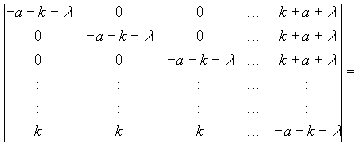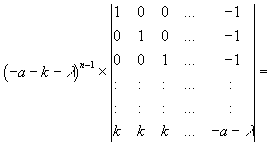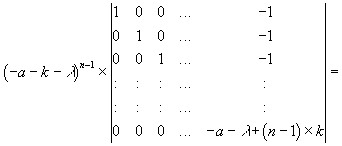(3.32)

(3.33)

(3.34)

(3.35)

(3.36)

Die erste Stabilitätsbedingung (3.34) ist immer erfüllt, weil die Parameter als positiv voarusgesetzt wurden. Die Bedingung (3.35) zeigt mathematisch, was wir auch rein gefühlsmäßig vermutet hätten: Die Staaten rüsten nicht auf, wenn sie sich so wenig bedroht fühlen, daß ihnen der finanzielle Aufwand viel zu groß erscheint. Der Sättigungskoeffizient ist sehr viel größer als der Bedrohungskoeffizient. Es zeigt sich auch, daß es linear von der Zahl der verfeindeten Staaten abhängt, um wieviel der Sättigungskoeffizient größer sein muß als die Bedrohungskoeffizienten. Und so wurde das Modell ja auch entworfen. Es wägt die klassischen Motive Furcht, Feindseligkeit und Sparsamkeit gegeneinander ab. Der stärkste Beweggrund bestimmt das Verhalten.

3.3 Vergleich der Modelle

Im Vergleich mit dem klassischen Modell von Richardson (1.20) sind alle in diesem Kapitel vorgestellten Modelle direkte Erweiterungen.

Die Gleichungen von (3.1) sind die direkte Erweiterung auf den dreidimensionalen Fall. Jede zweidimensionale Untermatrix, die das Verhältnis von zwei der drei Staaten zueinander beschreibt, weist die Struktur von (1.20) auf. In der Diagonale stehen die negativen Elemente, überall sonst die positiven. Jeder Staat ist mit jedem verfeindet, fühlt sich durch die Rüstung des anderen bedroht und reagiert mit der eigenen Rüstung. Es gibt stabile und instabile Gleichgewichtslagen, die nicht nur vom Vorzeichen der Koeffizienten, sondern auch von ihrer Größe abhängen. Wie in der Stabilitätsbedingung (1.34) ist es auch hier wichtig, daß die Sättigungsparameter größer als die Bedrohungsparameter sind. Die entsprechenden Kurven der Simulation sind einander sehr stark ähnlich. Der exponentielle Charakter der Lösungen bestimmt in beiden Fällen das Bild.

Das Modell (3.13) läßt sich als völlig äquivalent zu (1.20) betrachten. Fassen wir nämlich die beiden verbündeten Staaten als einen Staatenbund auf, so reduziert sich die Dimension auf zwei, und wir haben genau den Fall des ersten Kapitels. Der linke obere Block enthält nur negative Elemente. Wir können ihn als das negative "Diagonalelement" des Staatenbundes auffassen, das zweite negative Diagonalelement ist a₃₃. Die anderen Elemente sind wieder positiv, genauso wie es im klassischen Fall ist.

Der dritte Fall der beiden geheimen Allianzen kann ebenfalls als direkte Erweiterung von (1.20) aufgefaßt werden. Da der erste Staat mit jedem der beiden anderen verbündet ist, bleiben in Wirklichkeit nur zwei verfeindete Staaten übrig. Vernachlässigen wir also den ersten Staat und streichen die ersten Zeile und Spalte der Matrix bleibt eine zweidimensionale Matrix der klassischen Form über.

So wie (3.1) aus (1.20) hervorgegangen ist, kann die Gleichung für beliebig viele Staaten erweitert werden. Die Matrix von (3.26) hat weiterhin auch negative Diagonalelemente und alle anderen Elemente sind positiv. Das ist der allgemeinste Fall; wenn n = 2 ist, erhalten wir direkt die Gleichung (1.20), bei n = 3 die Gleichung (3.1). Sogar n = 1 läßt sich interpretieren als ein Staat, der ohne Feinde ist, und weil der einzige Koeffizient der Differentialgleichung sein Sättigungsparameter und daher negativ ist, rüstet er daher ab, bis der Rüstungsstand auf einem gewissen niedrigem Nieveau vom Wert g/a verbleibt.

Es zeigt sich also, daß das Richardsonmodell auf vielfältige Weise linear erweitert werden kann, und daß seine Erweiterungen sich auch verschieden deuten lassen. Die Grundstruktur bleibt jedoch immer die selbe: eine lineare Differantialgleichung, die den Rüstungstand der Feinde und der Freunde mit verschiedenen Vorzeichen versieht, mit entsprechenden Koeffizienten gewichtet und mit einem konstanten Summanden der Feindseligkeit auf die Rate der Aufrüstung wirken läßt. Das ist die geniale Grundidee, die sich an verschiedene Konstellationen anpassen und sich neu interpretieren läßt.

Kurzfassung und Inhaltsverzeichnis
Einleitung
1. Das Modell von Richardson
2. Das Modell von Intriligator und Brito
3. Lineare Erweiterungen des Richardson-Modells
4. Nichtlineare Erweiterungen des Richardsonmodells
5. Nichtlineare Erweiterung des Intriligator-Brito-Modells
Literaturverzeichnis