1. Das Modell von Richardson

1.1 Die Modellgleichungen

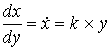
Das erste mathematische Modell eines Rüstungswettlaufes zwischen feindlichen Staaten wurde kurz nach dem ersten Weltkrieg von Lewis Richardson entworfen, fand jedoch zunächst keine Beachtung der Öffentlichkeit. 1953 starb Richardson, und erst sieben Jahre später wurde sein Modell veröffentlicht¹. Seitdem wuchs die Literatur zu diesem Thema immer mehr an, und die meisten der nachfolgenden Arbeiten beziehen sich auf Richardsons Ideen. Das Modell von Richardson ist das klassische Modell der Friedens- und Konfliktforschung. Es stellt den Rüstungswettlauf zweier Staaten mit Hilfe von zwei linearen Differentialgleichungen dar. Die Annahmen des Modells sind einfach und plausibel.

Richardson ging in seinen Überlegungen von folgenden Voraussetzungen aus: Er betrachtete zwei verfeindete Staaten und deren Verteidigungsbereitschaft. Jeder Staat fürchtet einen Angriff des anderen und hält seine militärischen Kräfte bereit. Diese Bereitschaft wird vom anderen Staat als Bedrohung ausgelegt, und der Kreis schließt sich. Das Bild des bewaffneten Feindes vor Augen, bemüht sich selbst ein friedliebendes Land um geeignete Mittel der Verteidigung. Einfach ausgedrückt heißt das: die einen rüsten auf, weil die anderen aufrüsten, und die anderen rüsten auf, weil es die einen tun.

Dieser einfache Zusammenhang läßt sich in der Sprache der Mathematik als ein System von zwei linearen Differentialgleichungen ausdrücken. Sei x der Stand der Rüstung im ersten Staat, y der im zweiten. Die Rate, mit der ein Staat aufrüstet ist die erste Ableitung des vorhandenen Rüstungsstandes. Wir nehmen an, daß die Aufrüstungsrate eines Landes von dem Rüstungsstand des anderen Landes abhängt und drücken das in den Differentialgleichungen mit Hilfe von positiven Proportionalitätsfaktoren k und l aus. Die Gleichungen bekommen die einfache Form:

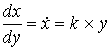(1.1)

(1.2)

Die beiden Konstanten k und l werden Bedrohungsparameter genannt.

Das lineare Differentialgleichungssystem kann leicht gelöst werden:

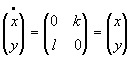(1.3)

Die Eigenwerte der Matrix erhalten wir aus der Gleichsetzung ihrer Determinante mit 0, der sogenannten Eigenwertgleichung.

(1.4)

(1.5)

(1.6)

Die Eigenwerte der Matrix des Differentialgleichungssystems sind die Koeffizienten der Exponenten der Lösungen. Die Zeit t läuft vom Zeitpunkt t₀=0 bis zu einem Zeitpunkt t=T, der nicht näher definiert ist. In dieser Zeitspanne [0, T] soll der "interessante" Teil der Lösung liegen. Für den positiven Zweig der Wurzel soll l stehen, für den negativen Zweig -l.

(1.7)

(1.8)

Die Werte von A, B, C und D müssen noch durch die Anfangswerte der Differentialgleichungen bestimmt werden. Über die Koeffizienten C und D läßt sich jedoch aussagen, daß sie von A und B abhängen.

(1.9)

(1.10)

Die Lösungen sehen zunächst so aus:

(1.11)

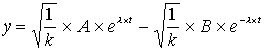(1.12)

Ihre endgültige Gestalt erhalten die Lösungen, wenn die Anfangswerte x₀ und y₀ mitberücksichtigt werden.

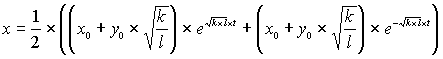(1.13)

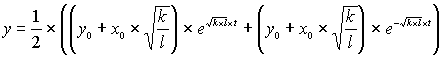(1.14)

Wenn zum Beispiel die Koeffizienten k und l identisch sind und beide Staaten zum Zeitpunkt t₀=0 mit dem gleichen Potential an Waffen ihren Rüstungswettlauf beginnen, also x(0) = x₀ = y(0) = y₀, dann vereinfachen sich die Formeln und die Waffenansammlungen beider Staaten wachsen exponentiell an.

(1.15)

Dieses erste, einfache Modell ist wegen des unbeschränkten Wachstums seiner abhängigen Variablen nicht besonders realistisch. Vielleicht können wir diesen starken Anstieg der Rüstungsausgaben als Krieg interpretieren. Führen wir nun einen einschränkenden Effekt in unser Modell ein. Je mehr Waffen ein Staat schon lagert, desto weniger könnte er interessiert sein an einem weiteren Ankauf beziehungsweise an weiterer Produktion. Die Wachstumsrate wird durch das schon vorhandene Potential gebremst. In unseren Gleichungen sieht das so aus:

(1.16)

(1.17)

Die beiden Koeffizienten a und b beschreiben den Einfluß der Ermüdung im Rüstungswettlauf, der übermäßigen Kosten der Rüstungsausgaben oder den mit der Anzahl der Waffen zunehmenden Glauben an die eigene Stärke und heißen daher Sättigungsparameter. Sie sind beide positiv. Ein wichtiger Bestandteil fehlt noch in unserem Modell. Staaten rüsten ja nicht nur aus Furcht vor anderen auf, sondern auch deshalb, weil sie mit den anderen Staaten verfeindet sind. Die menschlichen Gefühle, Haß und Feindseligkeit, wirken als Feindseligkeitsparameter in Form einer positiven Konstanten auf die Rüstungsrate ein. Damit erhält das Modell seine endgültige Form:

(1.18)

(1.19)

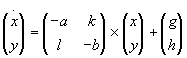(1.20)

Mit der Transformation um die Gleichgewichtslage (1.29) und (1.30) berücksichtigen wir zunächst die Inhomogenität. Um die Lösung des homogenen Systems zu finden, suchen wir die Eigenwerte der Matrix.

(1.21)

Aus der charakteristischen Gleichung ergeben sich die beiden Eigenwerte.

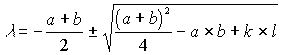(1.22)

Die Lösungen sind also Linearkombinationen von Exponentialfunktionen mit den Exponenten l₊´t beziehungsweise l_-´t. Die Koeffizienten der Lösung von y hängen jedoch von den Koeffizienten von x ab, und die Lösungen erhalten die allgemeine Gestalt:

(1.23)

(1.24)

Jetzt brauchen nur noch die Koordinaten rücktransformiert und die Anfangswerte x₀ und y₀ berücksichtigt werden, dann erhalten wir die expliziten Lösungen.

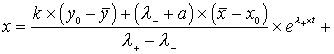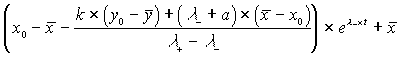(1.25)

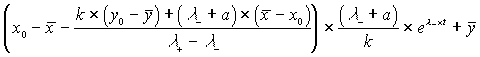(1.26)

1.2 Kausalschleifen

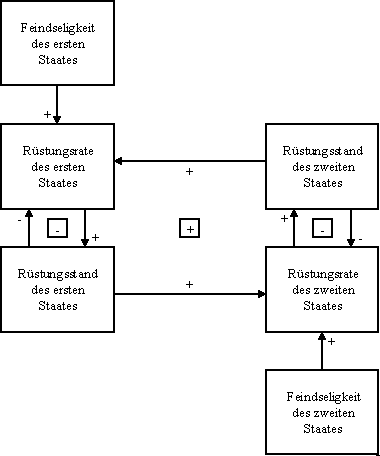
Abbildung 1.1 Darstellung des Modells durch Kausalschleifen

In diesem Modell finden wir zwei negative Rückkopplungen, nämlich dort, wo die schon erfolgten Rüstungsausgaben auf die Aufrüstungsrate einen beruhigenden Einfluß nehmen. Leider gibt es auch eine positive Rückkopplung, die den Zusammenhang der beiden Staaten darstellt. Hier besteht die Gefahr, daß der Rüstungswettlauf eskaliert.

1.3 Gleichgewichtslagen und Stabilität

Die Gleichgewichtslage einer Differentialgleichung erster Ordnung ist definiert als jener Punkt, an dem die erste Ableitungen der abhängigen Veränderlichen 0 sind. An diesem Punkt gibt es also kein Wachstum, keine Veränderung der Werte.

(1.27)

(1.28)

Die beiden Gleichungen können wir als Beschreibung zweier Geraden in der -Ebene interpretieren. Ihr Schnittpunkt, die Gleichgewichtslage des Differentialgleichungssystems, ist der Punkt mit den Koordinaten

(1.29)

(1.30)

Interessant ist auch die Stabilität dieser Gleichgewichtslage. Sie hängt vom Verhältnis der Anstiege der beiden Geraden ab, die sich aus den rechten Seiten der Differentialgleichungen durch Gleichsetzung mit 0 ergeben.

(1.31)

(1.32)

Angenommen, die erste Gerade (1.31) ist steiler als die zweite (1.32); der zugehörige erste Staat kontrolliert nur seine eigenen Rüstungsausgaben, die Variable x. In gleicher Weise beeinflußt der zweite Staat y. Jeder Staat versucht nun, den gegenwärtigen Stand auf die eigene "Gleichgewichtsgerade" zu bringen, und so erreichen beide Staaten gemeinsam die Gleichgewichtslage . In dem Bereich oberhalb von (1.31) ist die erste Ableitung von x größer als 0, unterhalb ist sie kleiner als 0. Rechts von der Geraden (1.32) ist die Ableitung von y positiv, links von ihr negativ. Startet der Rüstungswettlauf also etwa in einem Punkt rechts oberhalb vom stationären Punkt, so ist < 0 und < 0, die Werte von x und y werden kleiner, und die Trajektorie nähert sich der Gleichgewichtslage. Das ist der Fall, den die Abbildung 1.2 illustriert.

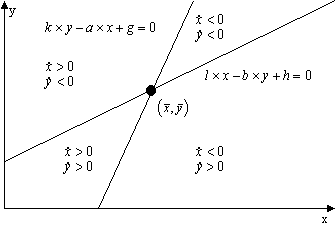
Abbildung 1.2 Stabiles Gleichgewicht

Im zweiten Fall ist der Anstieg der zweiten Geraden (1.32) größer als der der ersten, (1.31). Das Bemühen der einzelnen Staaten ist wie oben, den bestehenden Punkt auf ihre Gerade zu bringen. In diesem Fall führen ihre Bemühungen aber zu einer Entfernung des Standes von der Gleichgewichtslage . Sie ist also instabil, was die Abbildung 1.3 veranschaulicht. Startet die Trajektorie wieder in einem Punkt des rechten oberen Teilbereichs der Ebene, so liegt dieser Punkt diesmal rechts von (1.32) und oberhalb von (1.31), beide ersten Ableitungen sind positiv, die Trajektorie strebt ins Unendliche.

Wenn der Anstieg der ersten Geraden größer ist als der der zweiten, so ist (1.34) die Bedingung der Koeffizienten für Stabilität.

(1.33)

(1.34)

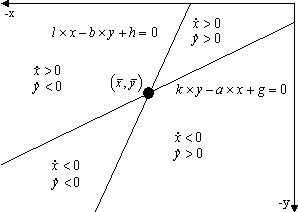
Abbildung 1.3 Instabiles Gleichgewicht

Ein interessantes Detail ist die Tatsache, daß im stabilen Fall der Nenner von und positiv ist, und weil der Zähler sicher positiv ist, liegt die stabile Gleichgewichtslage daher im ersten Quadranten. Das ist der Fall, der für die Praxis von Bedeutung ist.

Uns interessieren ja nur positive Werte von x und y, die wir als reale Rüstungsausgaben interpretieren können. Im instabilen Fall sind und negativ, die Gleichgewichtslage liegt im dritten Quadranten und ist für uns unwichtig.

Andererseits wissen wir, daß ein stationärer Punkt eines linearen Differentialgleichungssystems asymptotisch stabil ist, wenn die Realteile aller Eigenwerte der Matrix negativ sind. Die Eigenwerte gehen nämlich als Koeffizienten der Exponenten in die Lösung der Differentialgleichung ein und bestimmen so wesentlich deren Verhalten.

Unser System hat die Form (1.20) Die Eigenwerte der Matrix sind in der Formel (1.22) dargestellt. Da a und b positiv sind, ist der erste Teil von (1.22) immer negativ.

(1.36)

Es bleibt noch die Diskriminante zu betrachten.

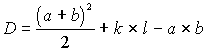(1.37)

Sie ist immer positiv, also läßt sich eine reelle Zahl als Wurzel berechnen. Interessant an dieser Zahl ist, ob sie dem Betrag nach größer oder kleiner als (1.34) ist. Daraus ergibt sich nämlich, ob beide Eigenwerte der Matrix negativ sind oder einer von ihnen positiv ist.

Durch den Ansatz der für die Stabilität erwünschten Ungleichung und durch algebraische Umformungen erhalten wir als Bedingung:

(1.38)

Die Ungleichung (1.38) ist mit der Ungleichung (1.33) identisch, und damit ist auch ihr rechnerischer Nachweis erbracht.

1.4 Implementation und Ergebnisse

Die Simulationssprache HYBSYS ist ein geeignetes Werkzeug, um schnell und einfach graphischen Lösungen von Differentialgleichungen zu erhalten. Die Gleichungen werden in Integralform in ein MODEL geschrieben. Die abhängigen Veränderlichen werden beim Ablauf des Programms als Funktion der Zeit berechnet und als Kurve gezeichnet. Die Parameter, die Koeffizienten der Gleichungen, können durch eine einfache Zuweisung im Experiment beliebig gewählt werden. Das MODEL für das Richardsonmodell sind in HYBSYS wie folgt aus.

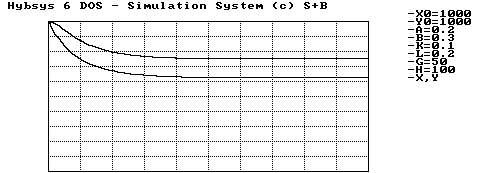
Abbildung 1.4 Stabiler Rüstungswettlauf, Abrüstung

Durch Experimente mit verschiedenen Parameterwerten erhalten wir auch verschiedene Kurven. Es gibt zwei Arten von Ergebnissen: entweder der Rüstungswettlauf ist stabil oder instabil.

Die Abbildung 1.4 zeigt einen Abrüstungsvorgang, bei dem beide Staaten exponentiell mit negativem Exponenten ihren Waffenvorrat abbauen. Ist die stabile Gleichgewichtslage einmal erreicht, so verändert sich die Lage nicht mehr. Mit den angeführten Parameterwerten ist die Bedingung (1.32) erfüllt.

An dieser Darstellung ist deutlich zu sehen, daß der stabiler Wert des Rüstungsstandes eines Landes über dem des anderen liegt. In der Praxis bedeutet das, daß ein Ungleichgewicht der Kräfte herrscht, aber dennoch ein Gleichgewicht im mathematischen Sinn vorliegt. Das Ziel der Abrüstung wäre also nicht die gleiche Anzahl an Waffen auf beiden Seiten, sondern eben so viele, daß beide Parteien zufrieden sind.

Besonders eindrucksvoll ist das Phasenbild dieses Falles. In der -Ebene streben alle Trajektorien dem Gleichgewichtspunkt zu. HYBSYS ermöglicht auf einfache Weise die Darstellung von Trajektorien mit verschiedenen Anfangswerten.

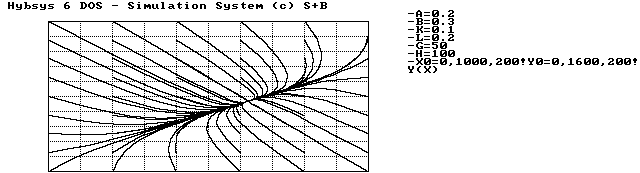
Abbildung 1.5 Stabile Gleichgewichtslage, Phasenbild

Die Abbildung 1.6 zeigt hingegen einen instabilen Rüstungswettlauf, der wahrscheinlich einen Krieg zur Folge hat. Das exponentielle Wachstum der Rüstung nimmt bedrohliche Ausmaße an. Die Parameter erfüllen die Stabilitätsbedingung (1.34) bei weitem nicht.

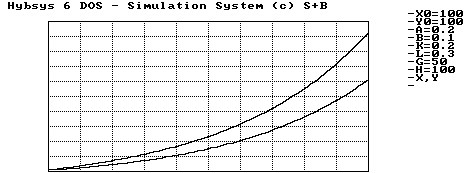
Abbildung 1.6 Instabiler Rüstungswettlauf

Auch bei diesem Rüstungswettlauf sehen wir die fehlende Symmetrie der Waffenarsenale. Die Staaten versuchen zwar gefühlsmäßig einander zu übertrumpfen, die Anzahl der vorhandenen Waffen eines Staates bleibt trotzdem immer unter der Anzahl des anderen. Es ist das fortgesetzte Weitersammeln an Waffen, das dem einzelnen Staat Beruhigung verschafft.

In Abbildung 1.7 ist nur der dritte Quadrant dargestellt, weil in ihm der instabile Gleichgewichtspunkt liegt. Die Trajektorien wenden sich ihm zunächst zu, biegen dann aber wieder von ihm weg und laufen ins Unendliche.

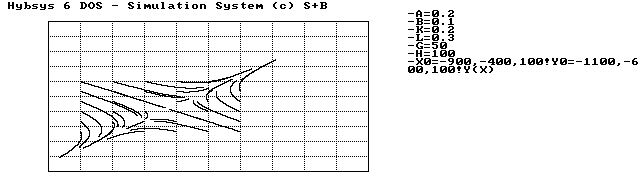
Abbildung 1.7 Instabile Gleichgewichtslage, Phasenbild

1.5 Das Rivalitätsmodell

Eine Abwandlung des klassischen Modells von Richardson ist das sogenannte Rivalitätsmodell. Die Überlegung geht davon aus, daß nicht der absolute Stand der feindlichen Rüstung für die eigene Aufrüstungsrate verantwortlich ist, sondern vielmehr der Vorsprung des feindlichen Rüstungsstandes vor dem eigenen. Die Aufrüstungsrate wird also von der Differenz des feindlichen Rüstungsstandes vom eigenen Rüstungsstand positiv beeinflußt. In den Modellgleichungen sieht das so aus:

(1.39)

(1.40)

Die Differentialgleichungen sind ebenfalls linear und das System ist mathematisch gesehen mit dem ersten identisch, nur die Koeffizienten sind verändert.

(1.41)

(1.42)

Der stationäre Punkt läßt sich leicht berechnen, entweder direkt als jene Werte von x und y, deren erste Ableitung 0 ist, oder noch einfacher aus den Formeln (1.29) und (1.30) durch Ersetzen von a durch a+k beziehungsweise von b durch b+l.

(1.43)

(1.44)

Der stationäre Punkt ist stabil, wenn die Parameter eine Bedingung erfüllen, die wir entweder durch Berechnen der Eigenwerte der Differentialgleichungsmatrix oder durch Einsetzen der neuen Parameter für a und b in die Formel (1.34) ermitteln können.

(1.45)

(1.46)

Das Modell sieht zwar in seinen Differentialgleichungen so aus wie das erste Modell (1.20) mit einer anderen Schreibweise der Sättigungsparameter. Genau diese größeren Sättigungsparameter machen es aus, daß dieses Modell immer assymptotisch stabil ist. Dadurch wird es unrealistisch und uninteressant.

1.6 Interpretation und Kritik

Wir haben gesehen, daß unter bestimmten Bedingungen der Rüstungswettlauf mathematisch instabil wird, die Werte von x und von y sich immer mehr vom stationären Punkt entfernen. Richardson interpretiert diese Situation als Krieg: unbeschränktes Wettrüsten bedeutet für ihn, daß ein Krieg bevorsteht. Der Schluß, daß vor einem geplanten Krieg eifrig gerüstet wird, ist einsichtig; aber gilt in jedem Fall die Umkehrung, daß auf Aufrüstung immer Krieg folgt?

Das Modell beinhaltet nicht direkt den Kriegsausbruch selbst. In den Feindseligkeitsparametern steckt zwar ein wenig Berücksichtigung der Menschen, aber sie berücksichtigen keine Änderung der internationalen Beziehungen, keine Fehlinformation oder sonstige Störungen, wie sie in der Realität vorkommen. Das Modell ist wahrscheinlich nicht sehr wirklichkeitstreu. Trotzdem ist es Richardson hoch anzurechnen, daß er als erster ein Differentialgleichungssystem gefunden hat, um diese Vorgänge zu beschreiben. Alle, die nach ihm arbeiteten, konnten sich auf seine ersten Ergebnisse stützen.

Die angenehmen Seiten des Modells sind seine mathematischen Eigenschaften. Die Differentialgleichungen sind linear mit konstanten Koeffizienten, also besonders einfach handhabbar. Die Lösungen lassen sich berechnen, und die beiden qualitativ verschiedenen Ergebnisse können wir plausibel interpretieren.

Kurzfassung und Inhaltsverzeichnis
Einleitung
1. Das Modell von Richardson
2. Das Modell von Intriligator und Brito
3. Lineare Erweiterungen des Richardson-Modells
4. Nichtlineare Erweiterungen des Richardsonmodells
5. Nichtlineare Erweiterung des Intriligator-Brito-Modells
Literaturverzeichnis